Introduction to Notch Filters
A notch filter, also known as a band-stop filter or band-rejection filter, is a type of electronic filter that attenuates signals within a specific frequency range while allowing signals outside that range to pass through relatively unaffected. Notch filters are designed to remove or suppress a narrow band of frequencies, making them particularly useful for eliminating specific noise or interference in a signal.
Applications of Notch Filters
Notch filters find applications in various fields, including:
- Audio signal processing: Removing unwanted hum or buzz from audio recordings, such as 50 Hz or 60 Hz power line interference.
- Telecommunications: Suppressing specific interference signals in wireless communication systems.
- Instrumentation: Attenuating specific noise frequencies in sensor measurements or control systems.
- Biomedical engineering: Removing power line interference or other noise sources from biomedical signals like ECG or EEG.
Types of Notch Filters
There are several types of notch filters, each with its own characteristics and design methods:
1. Passive Notch Filters
Passive notch filters are constructed using passive components such as resistors, capacitors, and inductors. They do not require an external power source and are relatively simple to design and implement. Passive notch filters are often used in low-frequency applications and can provide good attenuation at the notch frequency.
2. Active Notch Filters
Active notch filters incorporate active components like operational amplifiers (op-amps) in addition to passive components. They require an external power source but offer several advantages over passive notch filters, such as higher selectivity, sharper notch characteristics, and the ability to provide gain outside the notch frequency range.
3. Digital Notch Filters
Digital notch filters are implemented using digital signal processing techniques. They operate on digitized signals and can be realized using software algorithms or digital hardware like FPGAs or DSPs. Digital notch filters offer flexibility, programmability, and the ability to adapt to changing noise characteristics.
Notch Filter Design Techniques
1. Twin-T Notch Filter
The twin-T notch filter is a passive notch filter topology that uses a combination of resistors and capacitors to create a sharp notch at a specific frequency. It consists of two T-shaped networks: a series T-network and a parallel T-network. By carefully selecting the component values, a deep notch can be achieved at the desired frequency.
| Component | Series T-Network | Parallel T-Network |
|---|---|---|
| Resistor 1 | R | R |
| Resistor 2 | 2R | R/2 |
| Capacitor 1 | C | C |
| Capacitor 2 | C/2 | 2C |
The notch frequency (f_n) is given by:
f_n = 1 / (2π√(RC))
where R and C are the resistor and capacitor values, respectively.
2. Biquad Notch Filter
The biquad notch filter is an active notch filter topology that uses an op-amp and a combination of resistors and capacitors to create a second-order notch filter. The biquad notch filter offers adjustable notch depth and bandwidth, making it versatile for various applications.
The transfer function of a biquad notch filter is given by:
H(s) = (s^2 + ω_n^2) / (s^2 + (ω_n/Q)s + ω_n^2)
where ω_n is the notch frequency in radians per second, and Q is the quality factor that determines the notch bandwidth.
The component values can be calculated using the following equations:
R1 = R2 = R
R3 = R / (2Q)
C1 = C2 = 1 / (ω_n R)
3. IIR Notch Filter
Infinite impulse response (IIR) notch filters are digital filters that can be designed using various methods, such as the bilinear transform or the pole-zero placement technique. IIR notch filters have a recursive structure and can achieve sharp notches with low computational complexity.
The transfer function of a second-order IIR notch filter is given by:
H(z) = (1 – 2cos(ω_n)z^(-1) + z^(-2)) / (1 – 2rcos(ω_n)z^(-1) + r^2z^(-2))
where ω_n is the normalized notch frequency (0 < ω_n < π), and r is the pole radius that determines the notch bandwidth (0 < r < 1).
The filter coefficients can be calculated using the following equations:
b0 = 1
b1 = -2cos(ω_n)
b2 = 1
a1 = 2rcos(ω_n)
a2 = -r^2

Notch Filter Implementation
1. Analog Circuit Implementation
Passive and active notch filters can be implemented using analog circuits. The twin-T notch filter and biquad notch filter are examples of analog notch filter circuits. The component values are selected based on the desired notch frequency and bandwidth.
When implementing analog notch filters, it is important to consider factors such as component tolerance, temperature stability, and circuit noise. Proper layout and shielding techniques should be employed to minimize interference and ensure optimal performance.
2. Digital Filter Implementation
Digital notch filters can be implemented using software algorithms or digital hardware platforms. The IIR notch filter is an example of a digital notch filter that can be realized using difference equations or transfer functions.
Digital notch filters offer several advantages, such as the ability to adapt to changing noise characteristics, ease of tuning, and integration with other digital signal processing algorithms. However, they require analog-to-digital and digital-to-analog conversion, which can introduce quantization noise and latency.
When implementing digital notch filters, the sampling frequency, bit depth, and filter order should be carefully selected to achieve the desired performance while minimizing computational complexity and memory requirements.
Notch Filter Performance Metrics
Several performance metrics are used to evaluate the effectiveness of notch filters:
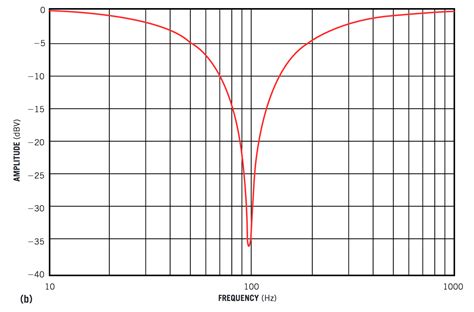
- Notch depth: The amount of attenuation provided by the filter at the notch frequency, typically expressed in decibels (dB).
- Notch bandwidth: The frequency range over which the filter provides significant attenuation, usually defined as the range where the attenuation is within 3 dB of the maximum attenuation.
- Quality factor (Q): A measure of the filter’s selectivity, defined as the ratio of the notch frequency to the notch bandwidth. Higher Q values indicate a narrower notch and better frequency selectivity.
- Passband ripple: The variation in the filter’s gain outside the notch frequency range, expressed in decibels.
- Stopband attenuation: The minimum attenuation provided by the filter in the stopband regions, which are the frequency ranges outside the notch bandwidth.
Notch Filter Design Considerations
When designing notch filters, several factors should be considered to achieve optimal performance:
- Notch frequency: The frequency at which the filter should provide maximum attenuation. The notch frequency should be accurately identified and specified based on the noise or interference characteristics.
- Notch bandwidth: The frequency range over which the filter should provide significant attenuation. A narrower notch bandwidth provides better selectivity but may require higher-order filters or more precise component values.
- Passband characteristics: The desired gain and ripple in the frequency ranges outside the notch bandwidth. The passband should be carefully designed to minimize distortion and ensure adequate signal transmission.
- Filter order: The number of poles and zeros in the filter transfer function. Higher-order filters provide sharper notch characteristics but may introduce greater complexity and potential stability issues.
- Component selection: The choice of components (resistors, capacitors, inductors, and op-amps) based on their tolerance, temperature stability, and noise performance. High-quality components should be used to minimize variations and ensure consistent filter behavior.
- Implementation platform: The choice between analog circuit implementation and digital filter realization based on the application requirements, available resources, and integration with other system components.
Frequently Asked Questions (FAQ)
1. What is the difference between a notch filter and a band-stop filter?
A notch filter and a band-stop filter are essentially the same things. Both terms refer to a filter that attenuates signals within a specific frequency range while allowing signals outside that range to pass through relatively unaffected. The term “notch filter” is often used when the stopband is particularly narrow, while “band-stop filter” can refer to filters with wider stopbands.
2. Can a notch filter completely eliminate noise at the notch frequency?
In theory, an ideal notch filter would provide infinite attenuation at the notch frequency, completely eliminating any noise or interference at that specific frequency. However, in practice, notch filters have finite attenuation, and the amount of noise suppression depends on factors such as the filter order, component quality, and implementation limitations. While notch filters can significantly reduce noise at the notch frequency, they may not completely eliminate it.
3. How do I choose the appropriate notch filter topology for my application?
The choice of notch filter topology depends on several factors, including the frequency range of operation, the required notch depth and bandwidth, the available components, and the implementation platform. Passive notch filters, such as the twin-T topology, are often used in low-frequency applications and can provide good attenuation with simple circuitry. Active notch filters, like the biquad topology, offer higher selectivity and the ability to provide gain outside the notch frequency range. Digital notch filters, such as IIR filters, provide flexibility and adaptability but require digital signal processing capabilities.
4. Can I cascade multiple notch filters to remove noise at different frequencies?
Yes, multiple notch filters can be cascaded to remove noise or interference at different frequencies. Each notch filter in the cascade will attenuate signals at its respective notch frequency, allowing you to target multiple noise components simultaneously. However, it is important to consider the overall system response when cascading filters, as the combined effect of multiple notches may introduce additional phase shifts or amplitude variations in the passband.
5. Are there any limitations or drawbacks to using notch filters?
While notch filters are effective at removing specific noise frequencies, they do have some limitations and drawbacks. Notch filters introduce phase shifts and group delay variations around the notch frequency, which can affect the timing and waveform of the signal. They also have limited attenuation outside the notch bandwidth, so they may not be effective against broadband noise or interference. Additionally, notch filters can be sensitive to component variations and temperature changes, which may cause the notch frequency to drift or the attenuation to degrade over time. Proper design, component selection, and calibration techniques can help mitigate these limitations.
Conclusion
Notch filters are essential tools for removing specific noise frequencies and improving signal quality in various applications. By understanding the different types of notch filters, their design techniques, and implementation considerations, engineers and technicians can effectively deploy notch filters to achieve the desired noise attenuation and signal integrity.
When designing notch filters, it is crucial to carefully consider the notch frequency, bandwidth, passband characteristics, filter order, component selection, and implementation platform. Proper design and implementation practices, along with an understanding of the filter’s limitations and trade-offs, enable the successful integration of notch filters into signal processing systems.
As technology advances, notch filter design techniques continue to evolve, offering new opportunities for noise suppression and signal conditioning. From classical analog circuits to advanced digital signal processing algorithms, notch filters remain a fundamental building block in the quest for clean, interference-free signals in a wide range of applications.
No responses yet